Die Quadratur des Kreises

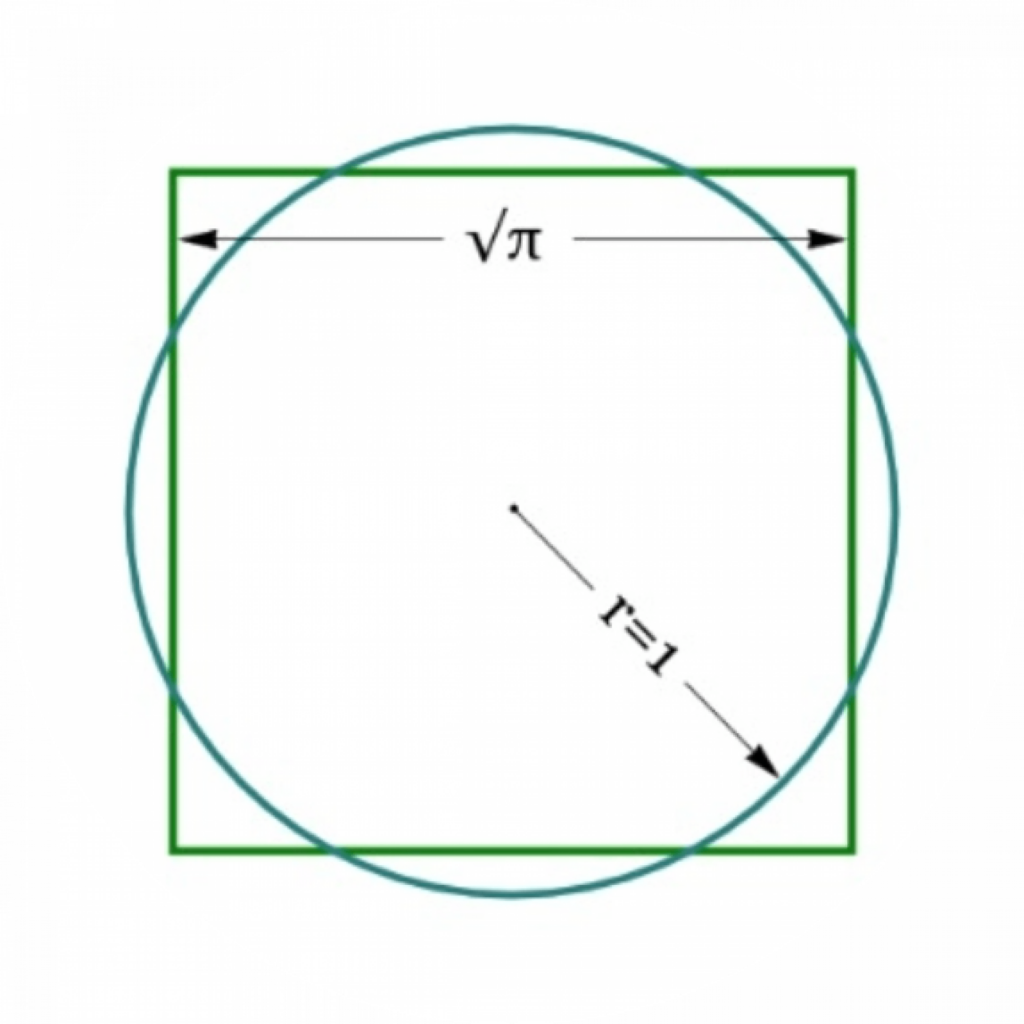
Ein Quadrat mit der gleichen Fläche wie ein Kreis mit Zirkel und Lineal konstruieren? Unmöglich. Das bewies der Freiburger Mathematik-Professor Ferdinand von Lindemann 1882 – und klärte damit eine uralte Frage der Geometrie.

Ob ein Spaziergang an der frischen Luft hilft, jahrhundertealte wissenschaftliche Rätsel zu lösen, an denen bereits antike Denker wie Anaxagoras (499–428 v. Chr.) oder der Universalgelehrte Leonardo da Vinci (1452–1519) scheiterten? Ferdinand von Lindemann, zwischen 1877 und 1883 Professor für Mathematik an der Universität Freiburg,¹hätte diese Frage sicherlich bejaht. Laut autobiographischer Notizen hat er 1882 auf einer Wanderung vom Freiburger Lorettoberg nach Günterstal entschlüsselt, warum die Quadratur des Kreises – also „mit Zirkel und (unmarkiertem) Lineal aus einem vorgegebenen Kreis ein Quadrat mit exakt demselben Flächeninhalt zu konstruieren“² – unmöglich ist³.

Dass die Kreisquadratur nicht funktioniert, ist auf verschiedene Eigenschaften der Kreiszahl Pi (π) zurückzuführen: Das Verhältnis von Kreisumfang zu Kreisdurchmesser wurde von dem griechischen Mathematiker Archimedes (ca. 287 v. Chr–212 v. Chr.) näherungsweise berechnet, lässt sich aber nicht als rationale Zahl ausdrücken. Letztere Erkenntnis geht auf den Universalgelehrten Johann Heinrich Lambert (1728–1777). ⁴ zurück. ⁵Die Leistung von Lindemanns lag darin, zu beweisen, „dass π darüber hinaus auch transzendent ist. Das heißt, dass es kein Polynom mit rationalen Koeffizienten gibt,“⁶ – wie zum Beispiel x³+2x-5 – „dessen Nullstelle π ist. Daraus folgt, dass es prinzipiell unmöglich ist, mithilfe geometrischer Konstruktionsschritte einen Kreis in ein flächengleiches Quadrat umzuwandeln.“⁷

Ferdinand von Lindemann steht stellvertretend für eine Reihe namhafter Forscher*innen, welche die Universität Freiburg als Stätte bedeutender wissenschaftlicher Erkenntnisse seit ihrer Gründung 1457 bis heute geprägt haben. An die Leistung des Mathematikers Ferdinand von Lindemann erinnert der bis heute verliehene gleichnamige Preis für herausragende Dissertationen in der Mathematik.⁸

Zurück zum Leitbild